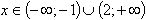1.5. Nevienādību un nevienādību sistēmu risināšana
a) Lineāru nevienādību risināšana.
Lineāru nevienādību risināšana sastāv no šādiem soļiem:
-
izdarot nevienādību ekvivalentus pārveidojumus, nevienādību pārvērš formā
ax < b; (ax > b; ax ≤ b;
ax ≥ b)
- atrisina nevienādību ax < b. Atkarībā no koeficientu a un b vērtībām un zīmēm iespējami šādi
gadījumi:
| ax < b |
| Nosacījumi |
Atrisinājums |
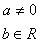 |
a > 0 |
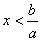 |
| a < 0 |
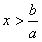 |
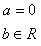 |
b > 0 |
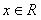 |
| b < 0 |
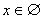 |
b) Kvadrātnevienādību risināšana.
Risinot kvadrātnevienādības, tiek izmantotas kvadrātfunkcijas y =ax2 + bx +
c īpašības. Kvadrātnevienādību risināšana sastāv no šādiem soļiem:
c) Nevienādību risināšana ar intervālu metodi.
Ar intervālu metodi var atrisināt nevienādības, kuras var pārveidot formā f(x)
> 0 (f(x) < 0; f(x) ≥ 0; f(x)
≤ 0) , (f(x) ir polinoms vai daļveida racionāla izteiksme). Šī metode pamatojas uz to, ka tiek aprēķinātas visas xvērtības, pie kurām izteiksmes f(x) vērtības var mainīt zīmi. Atrastās x
vērtības uz skaitļu ass veido intervālus. Atliek noskaidrot izteiksmes f(x)
zīmi katrā intervālā. Risinot nevienādības ar intervālu metodi, var izmantot šādu algoritmu.
| Risināšana ar intervālu metodi |
|
1) pārveido nevienādību formā f(x) > 0 (f(x)
< 0; f(x) ≥ 0; f(x) ≤ 0);
|
|
2) izteiksmi, kas atrodas kreisajā pusē, sadala lineāros vai kvadrātiskos reizinātājos;
|
|
3) iegūtos reizinātājus pielīdzina nullei un atrisina iegūtos vienādojumus; atrastos punktus, kuros izteiksme f(x) maina zīmi, atliek uz skaitļu ass;
|
|
4 a) uztverot katru reizinātāju kā funkciju, uzskicē to grafikus attiecībā pret x asi; saskaitot, cik funkciju grafiki ir zem x ass,
nosaka f(x) zīmi katrā intervālā;
Izteiksme f(x) ir sadalīta reizinātājos. Tās zīmi intervālā nosaka negatīvo reizinātāju skaits. Ja reizinātāju skaits ir nepāra skaitlis, izteiksmes zīme ir „-",bet ja reizinātāju skaits ir pāra skaitlis, izteiksmes zīme ir „+". Savukārt to, vai reizinātājs apskatāmajā intervālā ir negatīvs, nosaka tam atbilstošā grafika atrašanās zem x ass šajā intervālā.
|
4 b) izvēlas konkrētas vērtības katrā intervālā, ko veido atliktie punkti, un nosaka
f(x) zīmi šajā intervālā; |
| 5) nosaka intervālus, kuros ir spēkā dotā nevienādība. |
d) Nevienādību sistēmu risināšana.
Par nevienādību sistēmas atrisinājumu der skaitlis, kuru ievietojot visās sistēmas nevienādībās, iegūst patiesas skaitliskas nevienādības. Atrisināt nevienādību sistēmu nozīmē atrast visas tās mainīgā vērtības, kas der par atrisinājumu katrai sistēmas nevienādībai un pamatot, ka citu vērtību nav. Lai noteiktu nevienādību sistēmas atrisinājumu, var rīkoties šādi:
- vispirms atrisina katru nevienādību atsevišķi;
- pēc tam atrod nevienādību atrisinājumu kopu kopīgo daļu (jeb šķēlumu).
Praktiski ir izdevīgi katras nevienādības atrisinājumu attēlot uz vienas (vai katru uz savas) skaitļu ass; sistēmas atrisinājums ir visu atrisinājumu kopīgā daļa (jeb šķēlums)
e) Nevienādību ar moduli risināšana.
Risinot nevienādības ar moduli, var izmantot moduļa ģeometrisko interpretāciju.
Modulis ir attālums līdz 0.
|
Atrisināt nevienādību

Atbilde: 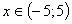
|
Atrisināt šo nevienādību nozīmē atrast visas tās mainīgā x vērtības, kuru attālums līdz 0 ir mazāks par 5 vienībām. To ilustrē šāds zīmējums.
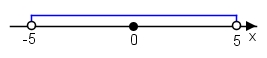
|
|
Atrisināt nevienādību
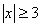
Atbilde: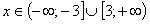
|
Atrisināt šo nevienādību nozīmē atrast visas tās x vērtības, kuru attālums līdz 0 ir lielāks par 3 vienībām. To ilustrē šāds zīmējums.

|
|
Atrisināt nevienādību
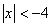
Atbilde: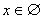
|
Atrisināt šo nevienādību nozīmē atrast visas tās x vērtības, kuru attālums līdz 0 ir mazāks par -4 vienībām. Tā kā modulis (attālums) ir pozitīvs lielums, tas nevar būt mazāks par negatīvu skaitli. Tātad, tādu x vērtību nav.
|
Risinot nevienādības ar moduli, var izmantot arī šādus ekvivalentus pārveidojumus:
Nevienādība ir ekvivalenta nevienādību sistēmai
ir ekvivalenta nevienādību sistēmai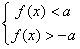
Piemērs
Atrisināt nevienādību 
|

|
Pāriet uz moduļa nevienādībai ekvivalentu nevienādību sistēmu
|
 |
Ar katru sistēmas nevienādību veic ekvivalentu pārveidojumu – abām pusēm pieskaita vienu un to pašu skaitli
|
 |
Ar katru sistēmas nevienādību veic ekvivalentu pārveidojumu – abas puses dala ar vienu un to pašu negatīvo skaitli
(-4) un maina nevienādības zīmi uz pretējo
|
Atbilde:
Nevienādība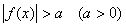 ir ekvivalenta nevienādībām
ir ekvivalenta nevienādībām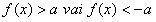
Piemērs
Atrisināt nevienādību |2x - 1| > 3
|
2x - 1 < -3 vai
2x - 1 > 3
|
Pāriet uz moduļa nevienādībai ekvivalentām nevienādībām
|
|
2x < -2 vai 2x > 4
|
Ar katru nevienādību veic ekvivalentu pārveidojumu - abām pusēm pieskaita vienu un to pašu skaitli
|
|
x < -1 vai x > 2
|
Ar katru nevienādību veic ekvivalentu pārveidojumu – nevienādību abas puses dala ar vienu un to pašu skaitli (2)
|
Atbilde: