5. uzdevums



A

 

Sporta svētkos notiek skrējiens maisos (uzklikšķini ar peli uz zīmējuma). Dalībnieks no punkta A aizskrien līdz pirmajam maisam, ielien tajā un lec atpakaļ uz punktu A. Izlīdis no pirmā maisa, tas skrien līdz otrajam maisam, ielien tajā un lec atkal atpakaļ un tā tālāk. Cik metrus veica dalībnieks:

a) kad atlēca ar ceturto maisu;

b) kad atlēca ar k-to maisu?

Atrisinājums

a) 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 = 20 (m)


Tālāk

b) Lai vispārinātu, jāsaskata likumsakarība, kā mainās noskrietais attālums (apzīmē ar ln ) atkarībā no tā, līdz kuram maisam (apzīmē ar n) jāskrien. Izsaka noskrieto attālumu dažām pirmajām n vērtībām.


Tālāk

n = 1   l1 = 1 + 1


Tālāk

n = 2   l2 = 1 + 1 + 2 + 2


Tālāk

n = 3   l2 = 1 + 1 + 2 + 2 + 3 +3


Tālāk

...

n = k   lk = 1 + 1 + 2 + 2 + 3 +3 +... + k + k

....


Tālāk

Noskrietie attālumi veido virkni (ln). Atbildēt uz jautājumu: cik metru veica dalībnieks, kad atlēca ar k - to maisu, nozīmē iegūt šīs virknes k – to locekli.


Tālāk

Var ievērot, ka lieluma lk skaitliskā vērtība ir iegūstama, aprēķinot divu vienādu aritmētisko progresiju summas

lk = 1+ 1+ 2+ 2 + 3 +3 +...+k + k = (1 + 2 + 3 +...+ k)+(1 + 2 + 3 +...+ k) = 2(1 + 2 + 3 +... + k)

Izmantojot aritmētiskās progresijas summas formulu iegūst, ka

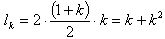
, kur a1- virknes pirmais loceklis, an - aprēķināmās summas pēdējais loceklis, n – summas locekļu skaits


Tālāk

Atbilde: Ja lk ir attālums, kuru ir veicis dalībnieks atlecot ar k – to maisu, tad lk = k + k2.