6.5. Plaknei perpendikulāra taisne, slīpne, slīpnes projekcija
Ja taisne krusto plakni, var būt divas iespējas – taisne ir perpendikulāra plaknei vai taisne nav perpendikulāra plaknei.
Ja taisne ir perpendikulāra divām krustiskām plaknes taisnēm, tad taisne ir perpendikulāra šai plaknei.
Piemērs.
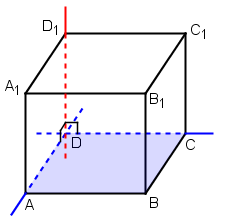
Taisne DD1 ir perpendikulāra taisnei DC un arī taisnei AD. Taisnes DC
un AD ir krustiskas un atrodas plaknē ABCD. Tātad taisne DD1ir perpendikulāra plaknei
ABCD (DD1 ABCD). ABCD).
|
|
Ja taisne nav perpendikulāra plaknei, tad no jebkura taisnes punkta iespējams novilkt perpendikulu pret plakni.Šādas (neperpendikulāras) taisnes nogriezni no jebkura tās punkta līdz krustpunktam ar plakni sauc par slīpni. Ja no viena punkta, kas atrodas ārpus plaknes, novelk gan perpendikulu, gan slīpni, tad nogriezni, kas savieno perpendikula un slīpnes galapunktus plaknē, sauc par slīpnes projekciju. Perpendikuls, kas novilkts no punkta pret plakni, ir īsākais attālums no punkta līdz plaknei.
Ja taisne nav perpendikulāra plaknei, tad tā veido ar plakni no 90° atšķirīgu leņķi. Par leņķi starp taisni un plakni sauc leņķi starp taisni un tās projekciju plaknē.
Piemērs
Taisne
D1B
attiecībā pret plakni
ABCD ir slīpne. Lai noteiktu leņķi starp
D1B un plakni
ABCD,
ir jāatrod taisnes
D1B
projekcija plaknē
ABCD. Tā kā
DD1
ir perpendikuls, kas novilkts no
D pret plakni
ABCD, tad slīpnes
D1B projekcija
ir
DB un meklētais
leņķis ir
 D1BD
D1BD.