N
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
R
S
T
U
V
Z
Neatkarīgi notikumi
Notikumu A sauc par neatkarīgu no notikuma B, ja notikuma A realizēšanās varbūtība nav atkarīga no tā, vai notikums B ir realizējies vai nav realizējies, t.i. ja P(A/B)=P(A), kurP(A)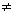 0 . Pretējā gadījumā notikumu A sauc par atkarīgu no B
0 . Pretējā gadījumā notikumu A sauc par atkarīgu no B
Neiespējams notikums
Par neiespējamu notikumu sauc notikumu, kas nevar realizēties nevienā mēģinājumā.
Nepārtraukti dati
Datus, kuru vērtība var būt jebkurš skaitlis no kāda intervāla sauc par nepārtrauktiem datiem.
Nesavienojami notikumi
Divus notikumus sauc par nesavienojamiem notikumiem, ja abi notikumi nevar realizēties (īstenoties) vienlaikus.
Nesavienojami notikumi
Ja notikumi A un B ir nesavienojami (nevar realizēties vienlaikus) tad notikuma A B varbūtība vienāda ar atsevišķo notikumu A un B varbūtību summu. P(A
B varbūtība vienāda ar atsevišķo notikumu A un B varbūtību summu. P(A B)=P(A)+P(B)
B)=P(A)+P(B)
Normālais sadalījums
Normālais sadalījums ir matemātisks jēdziens, kas raksturo nejaušībai pakļautu notikumu iestāšanās biežumu.
Nosacītā varbūtība
Notikuma A nosacīto varbūtību, ja B ir realizējies, apzīmē un sauc par notikuma A nosacīto varbūtību ar nosacījumu, ka B ir realizējies.
Notikuma varbūtība
Par notikuma varbūtību sauc skaitli, kas raksturo šī notikuma realizēšanās iespēju.
Notikuma A varbūtību apzīmē ar P(A), turklāt 0 ≤ P(A) ≤ 1.
Notikumu starpība
Par notikumu A un B starpību sauc notikumu, kurš realizējas tikai tad, ja ir iestājies notikums A, bet nav iestājies notikums B. To apzīmē A\B.
Notikumu summa
Par divu notikumu A un B summu jeb apvienojumu sauc notikumu, kurš realizējas tad un tikai tad, ja iestājas vismaz viens no notikumiem A un B. To apzīmē: A B vai A+B.
B vai A+B.
Notikumu šķēlums
Par divu notikumu A un B šķēlumu jeb reizinājumu sauc notikumu, kurš realizējas tikai tad, ja realizējas gan notikums A, gan notikums B. To apzīmē: ar A B vai A·B.
B vai A·B.