4. uzdevums

Četrstūra piramīdas MABCD pamats ir rombs ABCD, kura šaurais leņķis 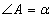 . Šķautne MA ir piramīdas augstums un ir divas reizes īsāka nekā romba mala.
. Šķautne MA ir piramīdas augstums un ir divas reizes īsāka nekā romba mala.
Aprēķini:
a) leņķus, kādus ar pamata plakni veido sānu šķautnes,
b) visus divplakņu kakta leņķus pie pamata!
Atrisinājums
a) Tā kā šķautne
MA ir perpendikulāra pamata plaknei, tad jānosaka leņķi, kurus veido šķautnes
MB,
MD un
MC ar pamata plakni.
Šķautņu
MB un
MD projekcijas
AD un
AB ir vienādas kā romba malas, un tādēļ šo šķautņu veidotie leņķi
 MBA
MBA
un
 MDA
MDA ir vienādi.
Tālāk
Taisnleņķa trijstūrī
MAD:

un

, kā arī
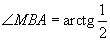 Tālāk.
Tālāk.
Šķautnes
MC veidoto leņķi var noteikt no

:
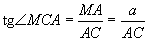 Tālāk.
Tālāk.

Nogriežņa
AC garumu var aprēķināt no romba
ABCD. Taisnleņķa trijstūra
ABO šaurais leņķis

, jo romba diagonāles ir savstarpēji perpendikulāras un ir romba pretējo leņķu bisektrises. Nogrieznis
AO =
AB · cos0,5
α = 2
αcos0,5
α
un
AC = 2 ·
AO = 4
αcos0,5
α
Tālāk.
b) Pavisam kopā ir četri divplakņu kakta leņķi – četru sānu skaldņu veidotie leņķi ar piramīdas pamata plakni, divi no tiem ir 90°- skaldnēm, kas satur šķautni
MA, jo tās ir perpendikulāras pamatam. Divi citi leņķi savā starpā ir vienādi ar leņķi

, jo tie ir simetriski attiecībā pret diagonāli
AC .
Tālāk.
Romba leņķis
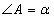
ir šaurs, tāpēc perpendikuls
AE atrodas ārpus romba . Pēc triju perpendikulu teorēmas arī
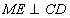
un skaldnes
MDC un pamata plaknes veidotais leņķis ir
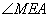
.
Tālāk.
Nogriežņa
AE garumu aprēķina no paralelograma
ABCD.
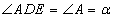
, jo
AB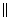 DC
DC un no
trijstūra
ADE 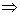

un no trijstūra
MEA iegūst, ka
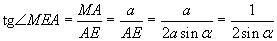
un .