1.3. Nevienādību veidi
Lineāras nevienādības
Nevienādības, kuras ar ekvivalentu pārveidojumu palīdzību var pārvērst par nevienādībām:
ax < b; ax > b; ax ≤ b;
ax ≥ b
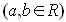sauc par lineārām nevienādībām ar vienu mainīgo x.
Piemērs.
Piemēram, nevienādības 2x-4 ≤ 0; 5x>0; -x-6 ≥ 0; x2-3x > x2+5 ir lineāras nevienādības.
Kvadrātnevienādības
Nevienādības, kuras ar ekvivalentu pārveidojumu palīdzību var pārvērst par nevienādībām:
ax2 + bx
+ c > 0; ax2
+ bx + c ≥ 0; ax2
+ bx + c < 0; ax2 + bx + c ≤ 0;
kur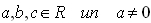 
sauc par kvadrātnevienādībām ar vienu mainīgo x.
Piemērs.
Piemēram, nevienādības x2
< 25; (x - 1) (x + 3)>2; 3x2
+ x <2x2
+ 6 ir kvadrātnevienādības.
Daļveida racionālas nevienādības
Nevienādības, kuras ekvivalentu pārveidojumu rezultātā var pārveidot formā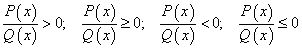
, kur
ir polinomi, sauc par daļveida racionālām nevienādībām. Ja nevienādība, kas satur daļveida racionālas izteiksmes, šādā formā nav dota, tad to var pārveidot, izmantojot arī izteiksmju identiskos pārveidojumus (piemēram, saucēju vienādošanu).
Piemērs.
Piemēram, nevienādības
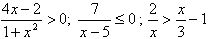
ir daļveida racionālas nevienādības.
Nevienādības, kas satur moduli
Nevienādību sauc par nevienādību ar moduli, ja mainīgais atrodas zem moduļa zīmes, piemēram, jebkura no nevienādībām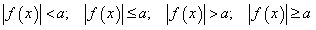
, kur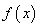 
ir polinoms vai daļveida racionāla izteiksme ir nevienādība ar moduli.
Piemērs.
Piemēram, nevienādības
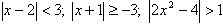
ir nevienādības, kas satur moduli.