3. uzdevums
Riņķī, kura rādiuss ir 3 cm, ievilkts taisnleņķa trijstūris, kura īsākā katete ir vienāda ar riņķa līnijas rādiusu. Kāda varbūtība, ka riņķī uz labu laimi atzīmēts punkts atradīsies trijstūra iekšpusē?
Atrisinājums
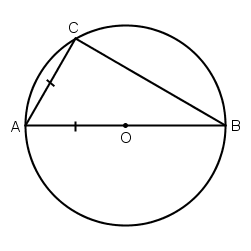
ΔABC
- taisnleņķa
AC = 3 cm, AB = 6 cm
CB
2 = 6
2 - 3
2
= 27
CB =
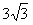
cm
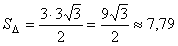
(cm
2)
Risinot uzdevumu, jāņem vērā, ka atzīmētais punkts ar vienādu varbūtību var atrasties jebkurā riņķa punktā. Varbūtība, ka punkts atradīsies riņķī ievilktajā trijstūrī, ir vienāda ar trijstūra laukuma attiecību pret visa riņķa laukumu.
Notikums A – uz labu laimi izvēlēts riņķa punkts pieder trijstūrim.
Labvēlīgo notikumu skaits ir
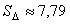 cm2.
cm2.
Visu iespējamo iznākumu skaits ir 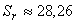 cm2.(skaidrojums)
cm2.(skaidrojums)
 (skaidrojums)
(skaidrojums)
Tālāk
Atbilde
Varbūtība, ka riņķī atzīmētais punkts atradīsies trijstūra iekšpusē, ir aptuveni 0,28.