6. uzdevums
Atrisini vienādojumu  ! Nosaki vienādojuma saknes intervālā x
! Nosaki vienādojuma saknes intervālā x (-2π;0)]!
(-2π;0)]!
Atrisinājums
Lai noteiktu vienādojuma saknes intervālā x
 (-2π;0], attēlosim šo intervālu vienības riņķī (skat. zīmējumu).
(-2π;0], attēlosim šo intervālu vienības riņķī (skat. zīmējumu).
Tālāk
Pēc zīmējuma varam spriest, ka dotajā intervālā atradīsies tikai viena vienādojuma sakne.
Ja n = 0, tad
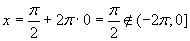 Tālāk
Tālāk
Ja n = -1, tad
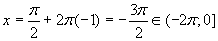
Ja n= -2, tad
 Tālāk
Tālāk
Izmanto redukcijas formulu

Izmanto redukcijas formulu sin(π + x) = -sinx
1 - sin2x -
sinx + 1 = 0
-sin2x - sinx + 2 = 0
sin
x
[-1;1]