2. uzdevums
Atrisini vienādojumu ar parametru m!
x
2 - 2(
m + 3)
x
+ 9 = 0
D = 22(m
+ 3)2 - 4·1·9 = 4(m2 + 6m + 9) -
36 = 4m2 + 24m
+ 36 - 36 = 4m2
+ 24m
Atrisinājums
Kvadrātvienādojuma atrisinājums ir atkarīgs no diskriminanta.
Šajā gadījumā D = 4m2+ 24m
Apskatam trīs gadījumus:
Tālāk
1) ja D < 0, tad vienādojumam atrisinājuma nav;
4m2 + 24m
< 0
 (paskaidrojums)
(paskaidrojums)
4m(m + 6) < 0
m1= 0; m2 = -6
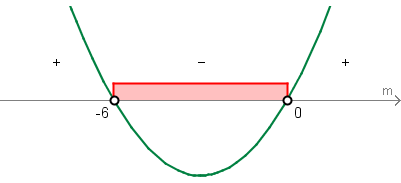
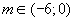
Tālāk
2) ja D = 0, tad vienādojumam ir tieši viena sakne;
4m2 + 24m
= 0
m1 = - 6; m2 = 0
Šī sakne ir:
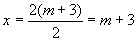
m1= - 6, tad
x = m + 3 = - 6 + 3 = - 3
m2 = 0, tad x
= m + 3 = 0 + 3 + 3
Tālāk
3) ja D > 0, tad vienādojumam ir divas dažādas saknes.
4m2 + 24m < 0
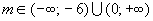
un
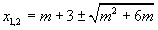 (paskaidrojums)
(paskaidrojums)
(paskaidrojums)
(paskaidrojums)
4m(m + 6) > 0
m1= 0; m2 = -6

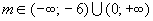
Atbilde
Atbilde
1) Ja 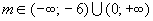 ,tad vienādojumam ir divas dažādas saknes:
,tad vienādojumam ir divas dažādas saknes: ;
;
2) ja m = - 6, tad vienādojuma sakne ir x = - 3 ;
3) ja 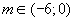 , tad vienādojumam atrisinājuma nav;
, tad vienādojumam atrisinājuma nav;
4) ja m = 0, tad vienādojuma sakne ir x = 3 .